StrEng007
Structural
- Aug 22, 2014
- 543
I'm having trouble illustrating the determinacy of this structure.
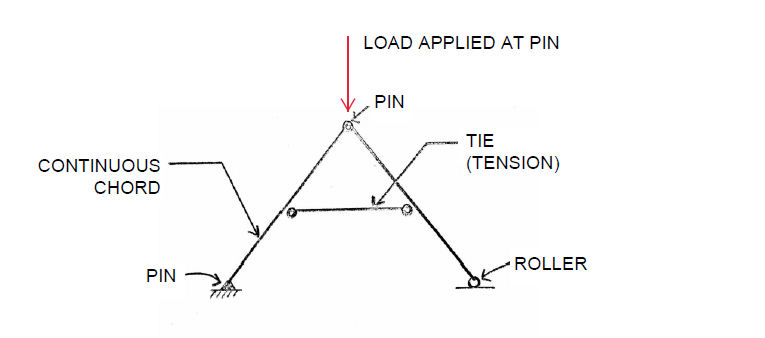
This is what I'm getting from determinacy checks if I treat it like a truss:
Treating the rafter as a continuous member,
b=3 (3 bars)
r=3 (3 support reactions)
b+r=6
2(j)=2(5)=10
6<10, unstable. This isn't correct, I believe this rafter is in fact stable.
Treating the rafter as two individual segments on each side,
b=5 (5 bars)
r=3 (3 support reactions)
b+r=8
2(j)=2(5)=10
8<10, unstable. Again, I don't believe this is correct.
Is there an exception that I'm missing?
This is what I'm getting from determinacy checks if I treat it like a truss:
Treating the rafter as a continuous member,
b=3 (3 bars)
r=3 (3 support reactions)
b+r=6
2(j)=2(5)=10
6<10, unstable. This isn't correct, I believe this rafter is in fact stable.
Treating the rafter as two individual segments on each side,
b=5 (5 bars)
r=3 (3 support reactions)
b+r=8
2(j)=2(5)=10
8<10, unstable. Again, I don't believe this is correct.
Is there an exception that I'm missing?

