Thought on element selection

[ebdoep2]

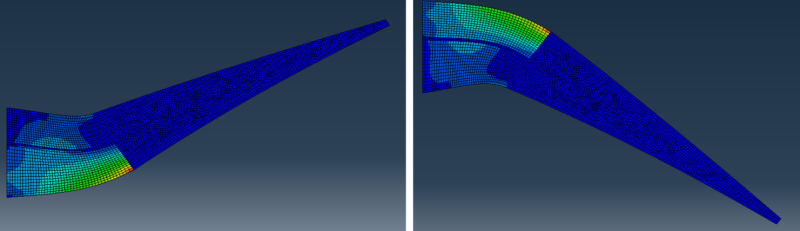
Before I get to the question, the background. I am solving a 2D plane strain problem. An attached image shows the typical deflections. There are multiple materials and a beam element runs almost horizontally down the center. I have a pretty good handle on what the different options on the elements mean, mathematically, but I am lost on what in practice is the difference and reason for selection. I have run the model with almost every combination and for one load case and see about a 2-3% difference mainly when changed from linear to quadratic in the plane strain elements. One of the materials has a poisson's ratio v=~0.5, so all elements are hybrid. So far I have tried.

For the planar portion
CPE8RH
CPE8H
CPE4H
CPE4IH

CPE6MH
CPE6H
CPE3H

For the Beam:
B22
B21
B23

The planar elements make up a majority of the structures stiffness. I have read through the manual but it can go back and forth on which elements are better for bending dominated problems (though I think since there are so many elements through the vertical direction, this is not bending dominated), which elements produce a more accurate result and etc. But again it gets very difficult to determine from its vague language what would be a good choice for me.

Since this is for an optimization study and not a super exact model, should I just call the %3 difference in elements insignificant and choose what gives me the best results, or convergence the best at large deflections?

More potentially useful information:
-NLGEOM on
-The model is used in optimization but the models solves quick enough that the expense of one element over another is not significant.

 

[ebdoep2]

I was really hoping someone would have some practical advise on this, hopefully with some insight beyond strictly the element definitions.

​