comhedoisl
Mechanical
- Apr 9, 2020
- 13
Hi all.
This is an interesting theoretical question from a book of Feodosiev - Advanced Stress and Stability Analysis. It reads like this:
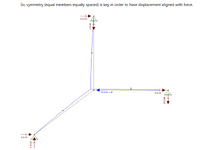
"A plane truss consisting of n>2 equal and equally spaced rods, connected in a common node, O.
The force P acts in the plane of the truss.
Show that the displacement of the node O is always directed along the force P and that the value of this displacement does not depend on the angle /alpha."
The book does provide an answer to this problem, but not with enough detail -- at least from my point of view. I'd like to have a more detailed discussion on this problem with other folks. Could you help me providing your insights?
**the blue circle is not part of the structure
Thanks.
This is an interesting theoretical question from a book of Feodosiev - Advanced Stress and Stability Analysis. It reads like this:
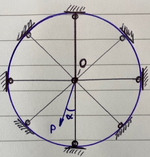
"A plane truss consisting of n>2 equal and equally spaced rods, connected in a common node, O.
The force P acts in the plane of the truss.
Show that the displacement of the node O is always directed along the force P and that the value of this displacement does not depend on the angle /alpha."
The book does provide an answer to this problem, but not with enough detail -- at least from my point of view. I'd like to have a more detailed discussion on this problem with other folks. Could you help me providing your insights?
**the blue circle is not part of the structure

Thanks.