Side wall contributing weld to rotating column 3

[YoungGunner]

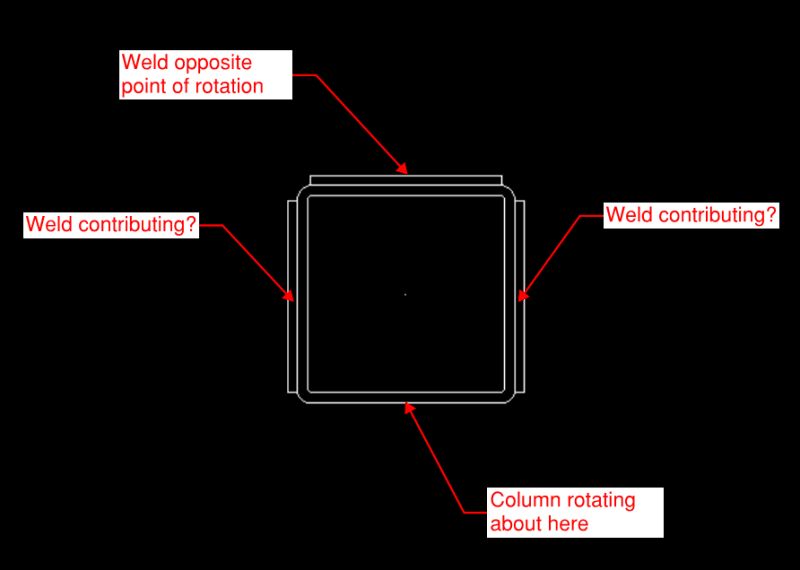
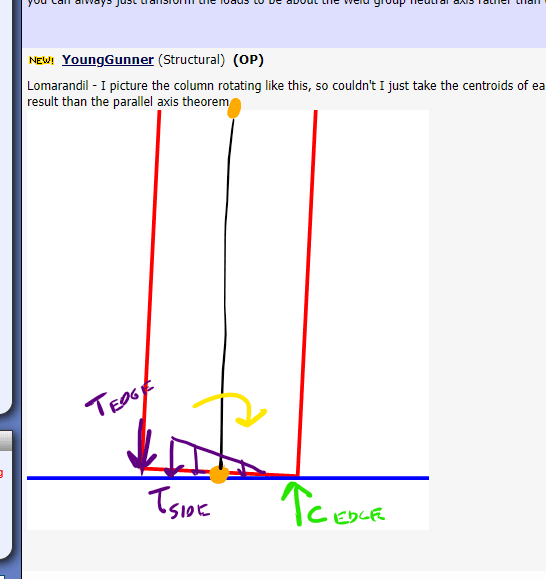
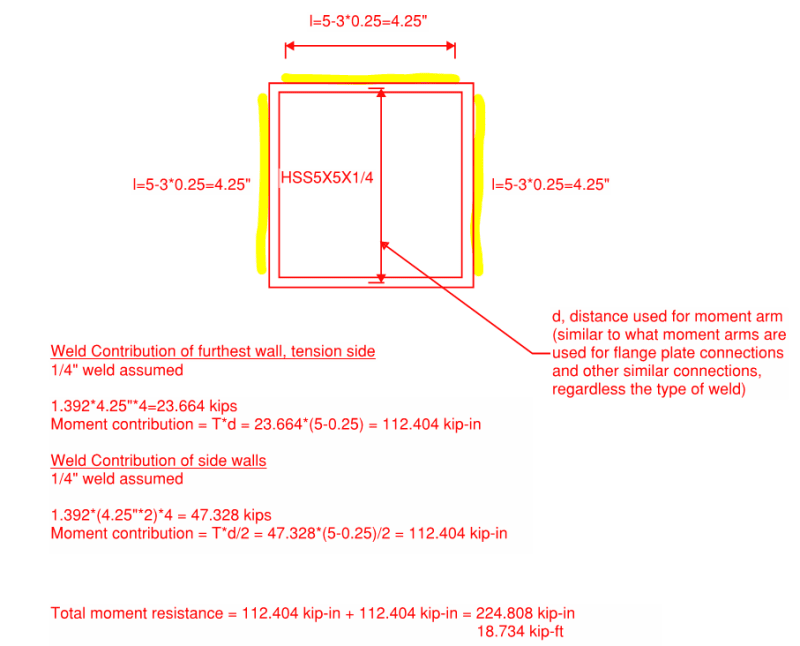
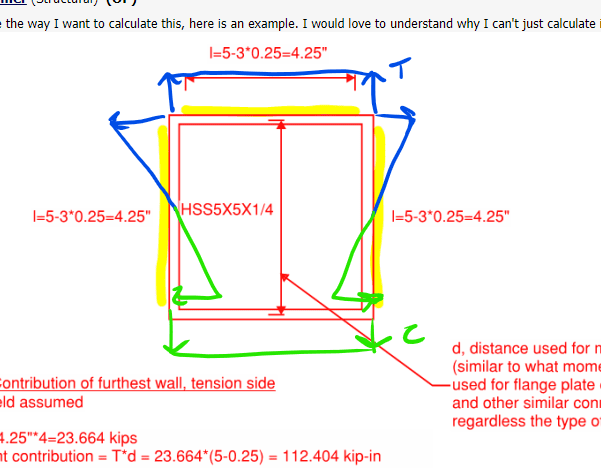
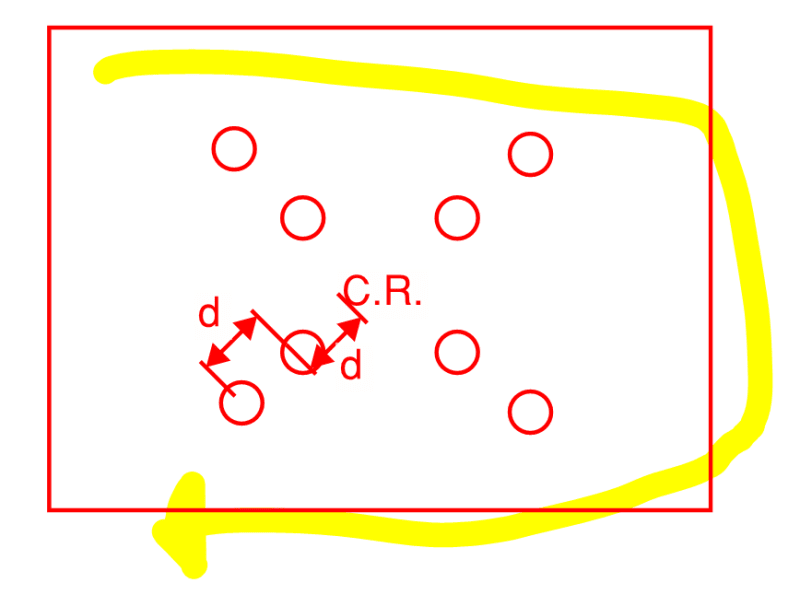
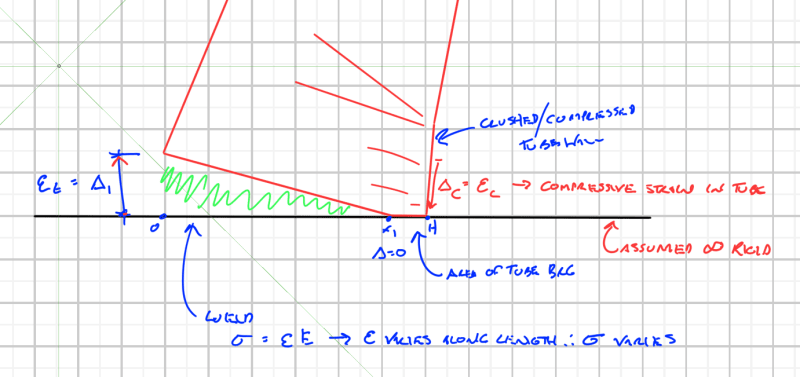
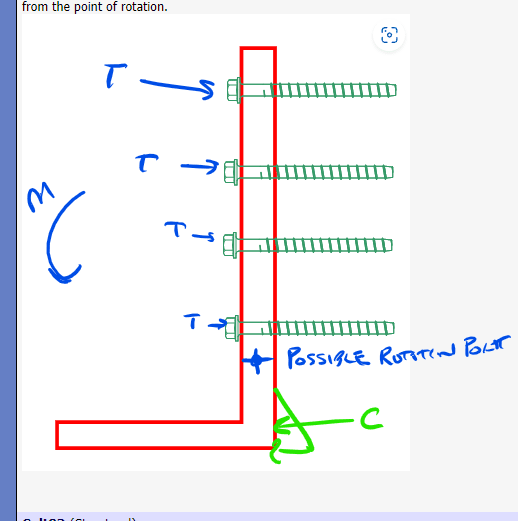
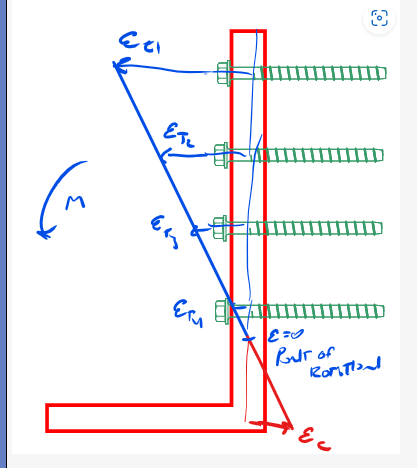
In relation to steel HSS welded to a base plate resisting a moment, I've noticed that Risa Connection only considers the column wall opposite the point of rotation to be effective for the weld strength. I'm curious if anyone thinks we can consider the side wall welds as contributing in resisting the moment as well?

 

[XR250]

Interesting. I have used the sidewall welds when I needed them to make the connection work out. The opposite weld def. does more of the heavy lifting though.

 

[Lomarandil]

Sure, you can use the section modulus of the combined weld group. Demand = M/S, if S is defined for a unit width line as b*d + d^2/3, then the demand is in kips/in. If these are fillet welds, you can take a boost to the capacity because the force is normal to the weld. Combine that with any other demand on the weld group (axial, shear) and you're good to go.

 

[Deker]

I agree with Lomarandil, except the directionality increase on fillet welds wouldn't apply because the weld is not loaded concentrically. Even it it were, there is new guidance recommending against the increase for square and rectangular HSS: Link #1, Link #2.

 

[noratetoobig]

Of course you can since they are all active, however. Since generally for simple design where it is assumed some welds carry the tension/compression loads from bending and some welds carry the shear (a simplified conservative approach), you would need to include both load actions(axial from axial and bending and shear) if designing as such.

As such, you would need to perform a von-mises stress calculation on the weld throats if they are fillet or part pen welds. Full penetration welds obviously would be the same as the plate thickness being welded.

 

[Lomarandil]

Thanks Deker, that's right. I had forgotten.

 

[YoungGunner]

Lomarandil - question on treating the weld as a line - isn't that equation based on the rotation about the neutral axis, but my situation is rotation about the base of the column. Does that equation apply here?

 

[Lomarandil]

I guess I don't understand what causes the base of the column to be the point of rotation. But with that assumption, correct, the equation I provided is somewhat conservative. Off the top of my head it may be b*d + d^2, but you should check that.

 

[Celt83]

you can always just transform the loads to be about the weld group neutral axis rather than doing the parallel axis theorem on the weld line properties.

 

[YoungGunner]

Lomarandil - I picture the column rotating like this, so couldn't I just take the centroids of each of the weld groups and their contribution is based on their distance from that point of rotation? This means each weld contribution is linear which would yield a different result than the parallel axis theorem.

 

[Celt83]

 

[YoungGunner]

To better illustrate the way I want to calculate this, here is an example. I would love to understand why I can't just calculate it this way.

 

[Celt83]

You've assumed uniform stress along the vertical side walls which violates strain compatibility. The stress profile in the side wall welds would more likely consist of both tension and compression.

 

[YoungGunner]

I guess I'm confused why the neutral axis is centered about the member in this case. For internal stresses and strains on the member itself, I understand why. But for my original column picture, ultimately that is what the "failed" version of the column looks like - tilting about one side, not the center. Technically you could look at my math as each tiny length of weld contributing linearly (thereby different strains) along the length of the side walls. Why is this wrong? I honestly appreciate your response and hope I can understand what you're talking about.

 

[driftLimiter]

The group of welds has its own neutral axis. When the weld group resists rotation, there will be a strain gradient about the neutral axis.

[ul]
[li]Your assuming a hinge location that is not aligned with the N.A. which incorrectly assumes all welds resist tension. In reality only some of the weld is resisting tension.[/li]
[/ul]

 

[driftLimiter]

But for my original column picture, ultimately that is what the "failed" version of the column looks like

The failed version of the column is now rotated about that point.

If the column didn't fail then it would not look like that anymore. In order to stay in the correct shape, the welds resist as a group in bending.

 

[YoungGunner]

This is starting to make some sense, but it presents the question - When you look at bolt groups resisting rotation, each bolt contributes linearly to resisting rotation based on their distance from the center of rotation. Assuming the outer bolts are twice the distance as the interior bolts, the outer bolts will take twice as much force. Why is this different than what we are discussing now?

 

[YoungGunner]

Maybe a better way of asking this question would be the example of a steel angle bolted to the side of a foundation wall. The point of rotation isn't the center of the bolt group right? It's the base of the angle. So each bolt is contributing linearly based on it's distance from the point of rotation.

 

[Celt83]

Bolts are point elements while welds are line elements, you could discretize the weld into tiny segments and follow a similar procedure.

 

[Celt83]

Remember statics Sum Fx = 0 which means Sum T = Sum C. You can sum moments about any point as long as you consider all of the applied loads, but the point of rotation is the point of 0 strain or said another way the point that has no translation in any direction under the applied loading.