LU decomposition

[hoshang]

Hi all,
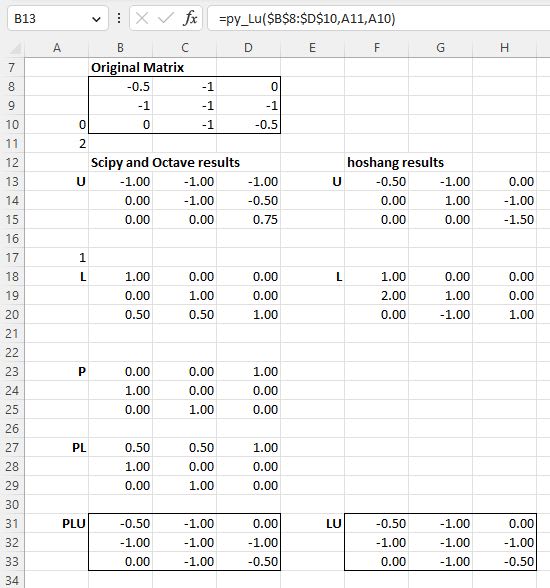
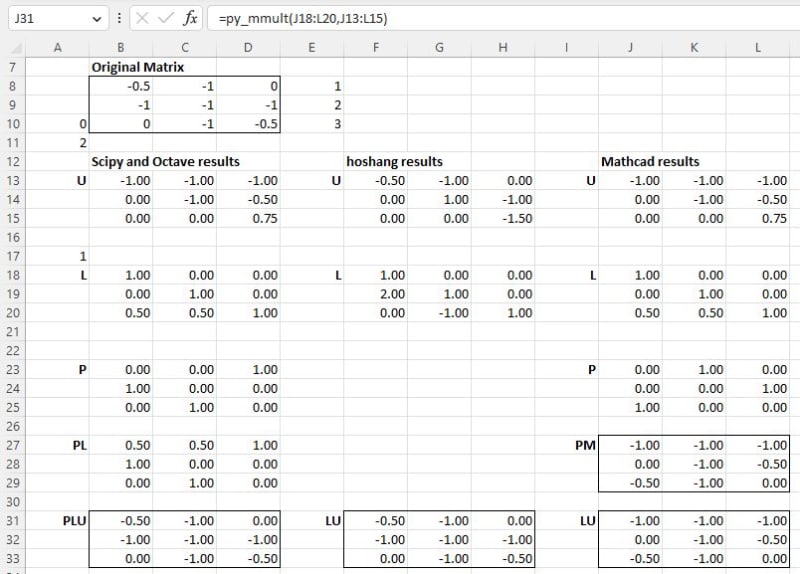
I wonder why LU for this matrix retrieves such LU decomposition result.
M=
-0.5 -1 0
-1 -1 -1
0 -1 -0.5

L=
1 0 0
0 1 0
0.5 0.5 1

U=
-1 -1 -1
0 -1 -0.5
0 0 0.75



While it should be:

L=
1 0 0
2 1 0
0 -1 1

 

[GregLocock]

I suggest you use a screenshot, smiley emoticons don't help.

Here's some Octave

>> M=[.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

-0.5000 1.0000 0
1.0000 0 0
0 0.6667 1.0000

U =

-1.0000 -1.0000 -1.0000
0 -1.5000 -0.5000
0 0 0.8333

>> M=[-.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

-0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

0.5000 0.5000 1.0000
1.0000 0 0
0 1.0000 0

U =

-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000
0 0 0.2500

>> M=[1.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

1.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

1.0000 0 0
-0.6667 1.0000 0
0 0.6000 1.0000

U =

1.5000 -1.0000 0
0 -1.6667 -1.0000
0 0 1.1000

>>


Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[hoshang]

Hi GregLocock,
thanks for your response. None of M matrix in your examples correspond to M in my example. Please try the M matrix in my example.

 

[GregLocock]

>> M=[-.5,-1,0;-1,-1,-1;0,-1,-0.5]
M =

-0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 -0.5000

>> [L,U]=lu(M)
L =

0.5000 0.5000 1.0000
1.0000 0 0
0 1.0000 0

U =

-1.0000 -1.0000 -1.0000
0 -1.0000 -0.5000
0 0 0.7500

Which is a very strange result, L is not triangular. Sorry I don't know enough about lu to explain what that means.


Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IDS]

Using the Scipy.Linalg LU function via Excel:

If I set permute_I to false I get the same as hoshang:
Lower =
1 0 0
-0 1 0
0.5 0.5 1

Upper =
-1 -1 -1
0 -1 -0.5
0 0 0.75

If I set permute_I to true I get the same as greg:
Permuted Lower =
0.5 0.5 1
1 0 0
-0 1 0

Upper =
-1 -1 -1
0 -1 -0.5
0 0 0.75

So greg's results give the permuted lower matrix. I'd have to remind myself of how these things work to know what you do with that.

Where did the values:
L=
1 0 0
2 1 0
0 -1 1
come from?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[GregLocock]

Of course the qick check is to do L*U, but we don't know what U is for
L=
1 0 0
2 1 0
0 -1 1

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IRstuff]

The results from Mathcad 14 are the same, and the extracted L, U, and P matrices behave as expected with P*M = L*U

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[hoshang]

Where did the values:
L=
1 0 0
2 1 0
0 -1 1
come from?

Thanks. Review any textbooks on LU decomposition. You will find out that the decomposition would be

L=
1 0 0
2 1 0
0 -1 1

U=
-0.5 -1 0
0 1 -1
0 0 -1.5

 

[IRstuff]

OK, so Mathcad's LU decomposition is a general purpose decomposition, see

https://www.cfm.brown.edu/people/dobrush/cs52/Mathematica/Part2/PLU.html

The function assumes that a permutation matrix P is required to make the decomposition work; this is why the lu() function returns 3 matrices.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[IDS]

OK, so it seems the answer to the question:
I wonder why LU for this matrix retrieves such LU decomposition result.
is that there is more than one way to decompose a matrix.

It seems that Scipy and Octave are using a pivotted lower matrix, so that for an original matrix A:
PLU = A
whereas for hoshang's matrices:
LU = A

Excel screen shot, calling Scipy fumctions:

Apparently Mathcad is doing something different, but I don't have Mathcad to see what is going on there.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IRstuff]

Mathcad is doing P*M = L*U, and the link I posted indicates that when LU decomposition is possible, there may be multiple solutions, and P in Mathcad's case is the inverse of the P in Doug's example, as can be seen below

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[IDS]

Thanks IRstuff

I have updated my spreadsheet to include the Mathcad way.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IRstuff]

This writeup goes into some more detail

https://math.unm.edu/~loring/links/linear_s08/LU

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[hoshang]

Hi all
So, how one can get hoshang results using Mathcad?

 

[IDS]

So, how one can get hoshang results using Mathcad?

I can't help with Mathcad, but why do you want to?


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

This link has a good detailed description of the procedures for forming and solving LU matrices, with and without pivoting:

https://courses.physics.illinois.edu/cs357/sp2020/notes/ref-9-linsys.html#

It has python code for each stage of the process.

At the moment I'm having trouble getting their lu_decomp function to work. If anyone get's it working, please let me know.

.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

At the moment I'm having trouble getting their lu_decomp function to work. If anyone get's it working, please let me know.

I have now got their code working. In the lu_decomp function:

Replace the two lines using np.block as below:

    # L = np.block([[L11, L12], [L21, L22]])
    # U = np.block([[U11, U12], [U21, U22]])
    L = np.zeros((n,n))
    U = np.zeros((n,n))
    L[0,0] = L11
    L[0,1:] = L12
    L[1:,0] = L21
    L[1:,1:] = L22

    U[0,0] = U11
    U[0,1:] = U12
    U[1:,0] = U21
    U[1:,1:] = U22

    return (L, U)

Also in the forward_sub function, replace:
for j in range(i-1):
with
for j in range(i):

With those changes the functions I tried seem to work correctly:
forward_sub
back_sub
lu_solve
lu_decomp

I haven't yet tried the functions using pivoting (but I'm working on it).

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[hoshang]

Hi,
What about my concerns?

 

[IDS]

Your original post has one questioned that has been answered in detail.

If you have remaining concerns perhaps you might tell us what they are.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IRstuff]

You're just going to have to do your own LU decomposition.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm