Undamped Response with Variable Springrate

[vibengrquest]

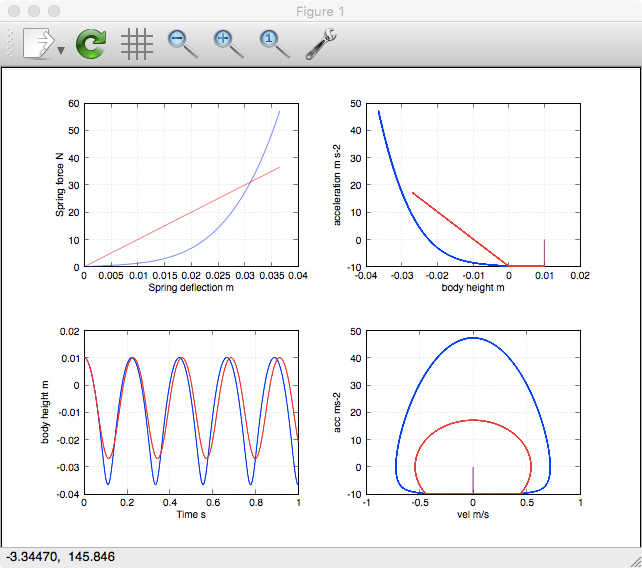
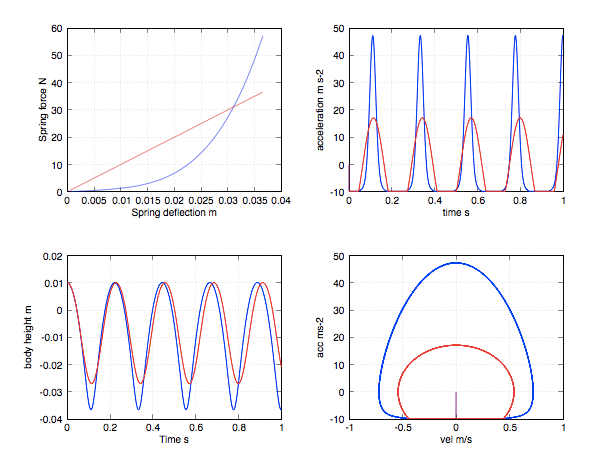
I'm trying to solve for the displacement of a mass with an applied constant load. Initially, there is a gap between the mass and spring, that is quickly overcome due to the applied force. The spring has a variable springrate. I have searched through multiple books and internet sites to find an example problem with a variable springrate and have had no luck. Again, this is an undamped case single degree of freedom case. Any suggestions?

 

[hacksaw]

Start by writing the force equations with a non-linear spring, it ha been dealth with from the mid 1800's on!

 

[FeX32]

The best way to solve a nonlinear vibration problem that also has a discontinuity (the gap) is numerically. Is the mass welded to the spring after it contacts it?
What software packages are you familiar with? Matlab, C-sharp?

I would solve this in Simulink.

Cheers,

 

[GregLocock]

That's quite a funny one because the mass will bounce free of the spring on every cycle. I'd solve it numerically, but I suspect an energy approach might lead to an analytical solution for some non linear stiffness curves.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[vibengrquest]

Thanks for the quick responses. GregLocock/ FeX32 the mass is will come from every cycle and is not joined to the spring. Out of the programs you listed, I have used Matlab back in college, any suggestions on how to set this up in Matlab and/or setup numerically?

Appreciate the help!

 

[GregLocock]

Yes. start with Newton. Work out the forces on the mass at each time step. That gives you an acceleration. Add a*dt to the velocity from the previous step. Add v*dt to the displacement from the previous step. Rinse and repeat. Test it on a linear spring and zero airgap first, that way you can check your answer analytically, w^2=k/m

That is rather inelegant and relies on very short dts but it will work.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[GregLocock]

I get that a 1 kg mass with a 0.004 m airgap and the following spring force=100.*displacement+30000000.*displacement.^4;

has a natural frequency of slightly more than 4 Hz and compresses the spring by about 35 mm.





Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[GregLocock]

Here's the results from a nice little script like the one you should have written by now.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[FeX32]

Greg,
The method you described you used is essentially the Euler numerical method.
I have also used it before with success and would recommend it.
Though, I have never used it to solve a DE that is discontinuous like this one is. When the mass is in the air it is governed by only gravity and we should expect there to be a clear discontinuity when it contacts the spring.
It would be most evident by plotting the force as a function of time.
This problem has intrigued me to an extent because I have in the past used the coefficient of restitution(COR) to model rigid body impact, and I am interested in the correlation of using COR vs. modeling a contact stiffness between the 2 bodies as they impact.

 

[GregLocock]

Here you are.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?