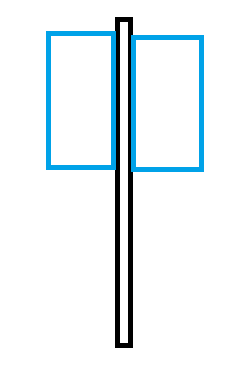ThomasH
Structural
- Feb 6, 2003
- 1,192
Hi all,
A colleague asked me something that I thought you might be able to help with.
If you look at the very simple figure below there is a support column (black) with diameter 1 m and height 30 m. Then you have two signs (blue) that are ~15 m high and the total width for the two signs and the column is 11 m.
The natural frequency is 0.9 Hz and the mass for the top part with column and sigh is ~1000 kg/m.
In the Eurocode EN 1991-1-4 (Wind) there is an appendix for "Vortex shedding and aerodynamic instability". There is a factor for galloping instability aG that becomes 0.4. That factor is a function of the depth and the width of the sign. The sign (a horizontal section) is a rectangular section with depth 0.7 m. That means that for the total width d/b = 0.7 / 11 = 0.06.
The table in Eurocode gives values for d/b = 2/3 to 1/3 and they are 1.0 to 0.4. But extrapolation is not permitted. If my colleague uses 0.4 (probably conservative) the result is that there is a risk for galloping. I have not found any source where I can get a better value for aG.
Does anybody have an idea for a solution without using extreme methods?
He is designing a sign post that is relatively large.
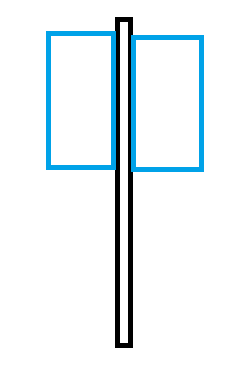
A colleague asked me something that I thought you might be able to help with.
If you look at the very simple figure below there is a support column (black) with diameter 1 m and height 30 m. Then you have two signs (blue) that are ~15 m high and the total width for the two signs and the column is 11 m.
The natural frequency is 0.9 Hz and the mass for the top part with column and sigh is ~1000 kg/m.
In the Eurocode EN 1991-1-4 (Wind) there is an appendix for "Vortex shedding and aerodynamic instability". There is a factor for galloping instability aG that becomes 0.4. That factor is a function of the depth and the width of the sign. The sign (a horizontal section) is a rectangular section with depth 0.7 m. That means that for the total width d/b = 0.7 / 11 = 0.06.
The table in Eurocode gives values for d/b = 2/3 to 1/3 and they are 1.0 to 0.4. But extrapolation is not permitted. If my colleague uses 0.4 (probably conservative) the result is that there is a risk for galloping. I have not found any source where I can get a better value for aG.
Does anybody have an idea for a solution without using extreme methods?
He is designing a sign post that is relatively large.