daparojo
Industrial
- Feb 25, 2010
- 36
Just a quick question, and grateful for any guidance.
I have an simple application that has 3 Bolts all have the same diameter, d, and has a slight clearance with the hole, D. They are responsible for clamping 2 plates together, or it could be 3 dependent on design.
They are tensioned, and a clamping force is exterted on the 2/3 plate surfaces, F.
A axial shear force, P is then applied to the joint.
The Plates are made from Steel.
The Shear Force Per Bolt = P / 3 (No. Bolts)
The Total Clamping Force on joint is = F x 3
If the joint was to move and slip and enter a bearing situation, then the Axial Shear Force has to be greater than the Total Clamping Force.
However, as there will be a co-efficient of friction between the plates i.e. 0.33 (Steel/Steel), then I presume that the total force to stop slippage would be Shear Load, P * Coefficient of Friction
Therefore if the Force to move the Joint that is under the Clamping Load must, then P x Co Eff Friction >= F.
Am I correct in my summation?
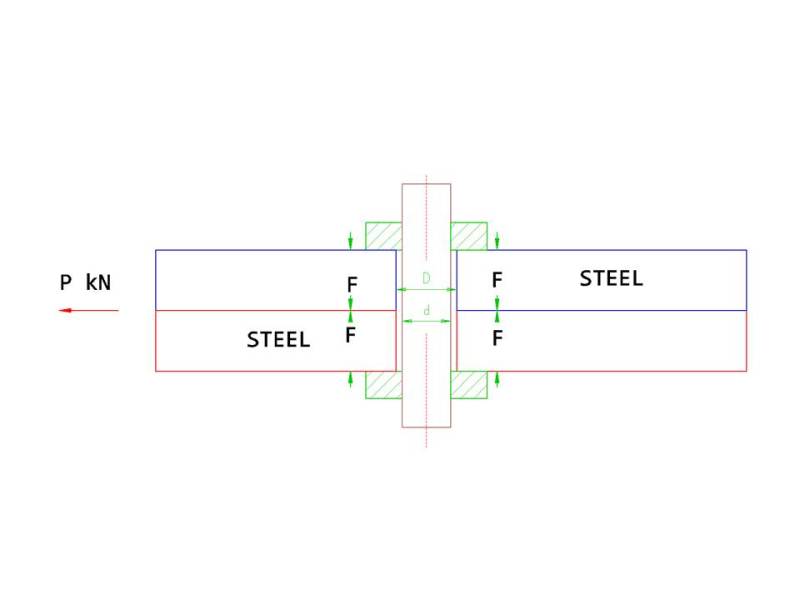
I have an simple application that has 3 Bolts all have the same diameter, d, and has a slight clearance with the hole, D. They are responsible for clamping 2 plates together, or it could be 3 dependent on design.
They are tensioned, and a clamping force is exterted on the 2/3 plate surfaces, F.
A axial shear force, P is then applied to the joint.
The Plates are made from Steel.
The Shear Force Per Bolt = P / 3 (No. Bolts)
The Total Clamping Force on joint is = F x 3
If the joint was to move and slip and enter a bearing situation, then the Axial Shear Force has to be greater than the Total Clamping Force.
However, as there will be a co-efficient of friction between the plates i.e. 0.33 (Steel/Steel), then I presume that the total force to stop slippage would be Shear Load, P * Coefficient of Friction
Therefore if the Force to move the Joint that is under the Clamping Load must, then P x Co Eff Friction >= F.
Am I correct in my summation?

