Amine A
Mechanical
- May 9, 2020
- 80
Hello,
I am coding the truss problem by finite element (figure below).I found difficulties at the level of the assembly of the stiffness matrices . Since the beams do not have the same materials, we will not have the same stiffness matrices. In the program , how to do the loop of assembly ? Any ideas please ?
I am coding the truss problem by finite element (figure below).I found difficulties at the level of the assembly of the stiffness matrices . Since the beams do not have the same materials, we will not have the same stiffness matrices. In the program , how to do the loop of assembly ? Any ideas please ?

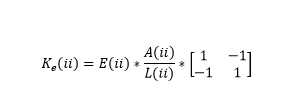
![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif)