Bending stiffness of concrete stair flight? 2

[Tomfh]

How do you guys assess the bending stiffness and deflection of concrete stairs?

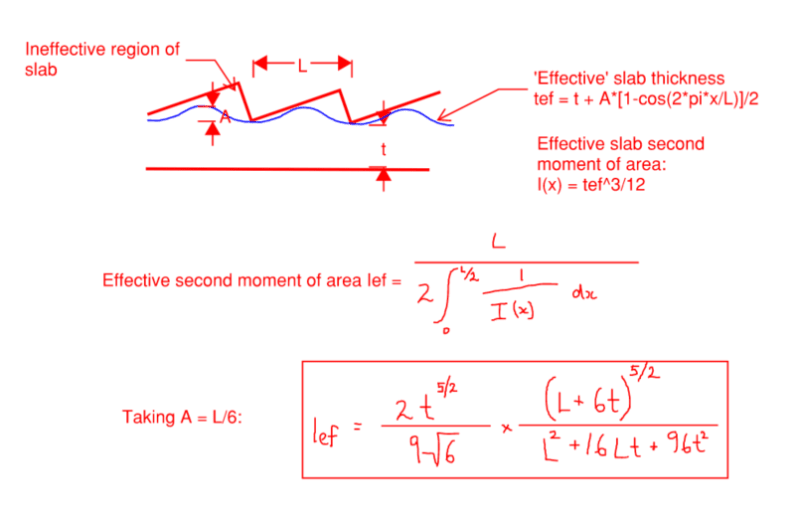
Typically I ignore the treads and use minimum thickness, and add the treads as dead load, however I wonder if this underestimates real stiffness? The concrete is in reality much thicker for much of the length.

 

[bugbus]

I was curious about this. My first thought was that the difference in stiffness would be very small.

I whipped up a quick FE model, it turns out to be fairly significant.

This is a 200 mm thick waist slab with 300 x 150 mm treads, based on a previous project I worked on.

The difference in stiffness (accounting for the additional weight of the treads) is 1.41x for the stairs compared to the 200 mm thick plain slab. Obviously it will be different depending on the actual geometry, and probably cracking would have some effect too.

The two other plots below are showing the principal (22) stresses, which clearly deviate into the tread portion.

 

[Tomfh]

Thanks for that. Useful results.

 

[KootK]

Typically I ignore the treads and use minimum thickness, and add the treads as dead load, however I wonder if this underestimates real stiffness?

I do the same. As gusmurr intimated, I suspect that both the strength and stiffness of the stair would be utterly dominated by the behavior at the cracks which will form between treads. Are the treads still worth something? Sure. Is it worth the computational effort to assess reliably? I doubt it. It seems to me that it would be akin to a version of the tension stiffening effect.

 

[bugbus]

I delved a little deeper into this.

If you consider that there is an effective portion of the slab that takes the form of a sine wave, which deviates above the waist of the slab by A = L/6 (as shown), this gives a really close prediction of the actual stiffness. (Why L/6? It just got me close to what I wanted )

For the example before, with L = sqrt(150^2 + 300^2) = 335 mm, and t = 200 mm, this gives an effective stiffness of 940,000 mm^4/mm, which is about 1.4x the stiffness of the 200 thick slab (666,667 mm^4/mm) as predicted by the FE model.

I agree with KootK that strength is determined at the thinnest part, but I think stiffness always takes on more of an average value. Even when it is cracked, the compression force will still deviate quite some way into the treads and increase the stiffness, maybe by a similar amount (~40%)?

 

[Tomfh]

For strength I'm sure we all agree the thickness as the neck governs.

For stiffness I agree the uncracked stiffness and deflection will resemble your approach.

However as Kootk points out, there is the cracked stiffness to consider. Maybe if it's cracking at the necks you end up with similar overall curvature as a regular cracked slab?